反向传播的思想
梯度下降
对于一个固定的函数,在其他变量不变的情况下,观测点沿着函数任一个自变量的负梯度方向移动就会使得观测点的函数值下降,同理同时沿着每个自变量的负梯度构成的负梯度方向移动,函数值就会很快的下降。
对于机器学习,一般的决策函数可以表示为$\hat y = f(x,\theta )$ 其中x是已知输入,y是输出,$\theta$ 是参数,但是在给定训练集和label时,其实自变量就是这个参数,我们的目标是找到一个合适的参数,让模型成为到我们想要的样子,所以我们把‘想要的样子’定义为与真实label 的差距,也就是目标函数,$L(y_i,\hat y_i)$ ,我们用它来衡量,模型与我们期望的差距,差距越小越好。所以目标函数可以看作是L为因变量,$\theta$ 是自变量,我们的终极目标是求L 的最小值时的 $\theta$ 的值。在预测是参数是固定的,此时自变量又变回了x.
所以参数的跟新与L的数值结果没有关系,只与它的导数以及当前参数值有关。
反向传播
其实传播只是一种通俗,形象的描述,其本质是链式法则,计算目标L对每个参数的导数,然后更新参数。
RNN 举例介绍反向传播
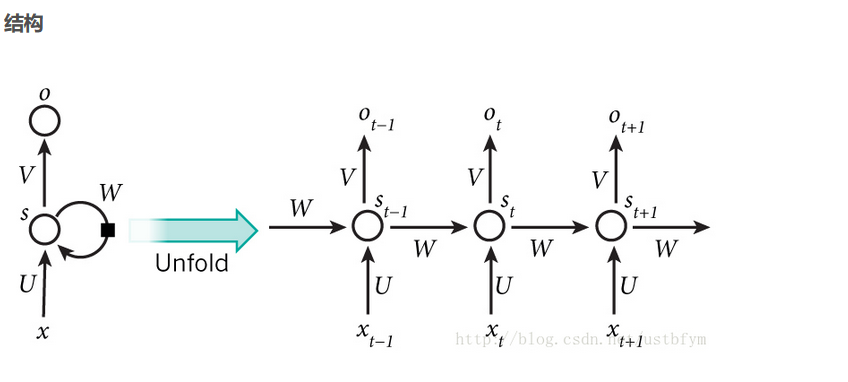
(由于参数W等是公用的,通过L的表达式可以得到每更新一次参数,就是把$L_t$ 的所有分量的梯度加起来)
反向对于参数(目前的自变量)W,V,U,b,c,,分别计算梯度,
从举例L最近的分别求导,
首先L 对$\hat y_i$ 求导,然后对c求导,按照一般的链式求导法则,很容易计算得到
当L是交叉熵,$\sigma$ 是softmax的时候,结果为:$\sum_t (\hat y_t- y_t)$
同理容易求得对V的导数。
比较难求的是W,U,b 这里以W为例,进行求解。
显然W的因变量是$h_t$ ,而$h_t$ 的因变量,有两个,一个是下一层的$L_{t+1}$ (因为影响了下一层的输入$h_{t+1}$) 另一个是这一层的$L_t$ 的. 所以L对于$h_t$的求导会有两个部分($h_t$对参数W,U,b 求导很简单,直接求导)
首先计算L对$h_t$的导数:
对于最后一层,T时刻,后续没有$h_{T+1}$所以:
当t小于T时,令
显然、$\frac{dh^t}{dW} =h_{t-1}$
所以对于,每个L分量$L_t$ 对W求导为:
所以
同理容易求得其他参数。
所以可以看出是每一个序列,更新一次RNN的参数。