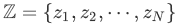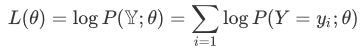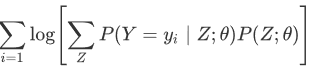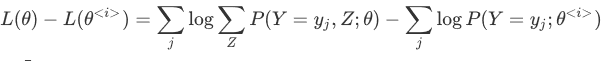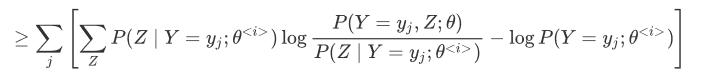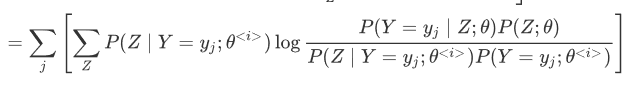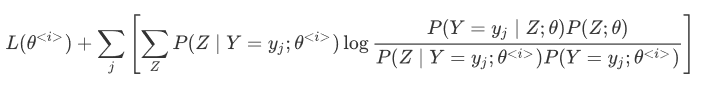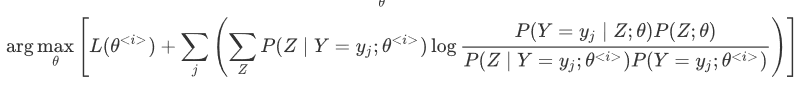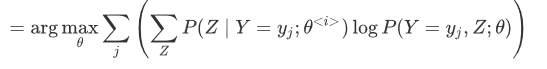EM 算法的部分知识点总结

问题介绍

一般的问题：
如果概率模型的变量都是观测变量，则给定数据之后，可以直接用极大似然估计法或者贝叶斯估计法来估计模型参数。
EM算法解决的问题：
存在一个中间过程，观测值是由两步随机过程得到的.

已知三枚硬币 A，B，C ，这些硬币正面出现的概率分别为。进行如下试验：先投掷硬币 A，若是正面则选硬币 B；若是反面则选硬币 C 。然后投掷被选出来的硬币，投掷的结果如果是正面则记作 1；投掷的结果如果是反面则记作0 。独立重复地次试验，观测结果为： 1,1,0,1,0,…0,1 。现在只能观测到投掷硬币的结果，无法观测投掷硬币的过程，求估计三硬币正面出现的概率。

其中第一次就是一个隐藏过程。

模型建立

已知最终的观测序列为假设隐藏层为
已知两个过程的模型$P_1,P_2$，但是不知道具体参数,参数集合为$\theta$。

通过极大似然估计的一般过程，目标函数为求公式的最大值：

其中Y 是与Z 有关系的变量，所以公式展开是：

其中$\theta$ 是两个过程中的所有参数。与一般问题不同的是含有隐藏过程Z ，而它是未观测数据。

模型求解

原理

目标：让$L(\theta)$ 迭代的越来越大,直到收敛
过程：

带入过程Z 得到新的目标

因为log是凸函数，通过jessen不等式得到目标函数的下界：

化简得到：

最终$L(\theta)$ 的下界为：

原问题转化为求上式的最大值时的$\theta$ 值。即：

化简（删除了常数项）为：

最终原问题转化为上述问题，其中$\theta$ 是下一次迭代的目标值（未知量），其他均为已知量。